最小二乘回归拟合直线

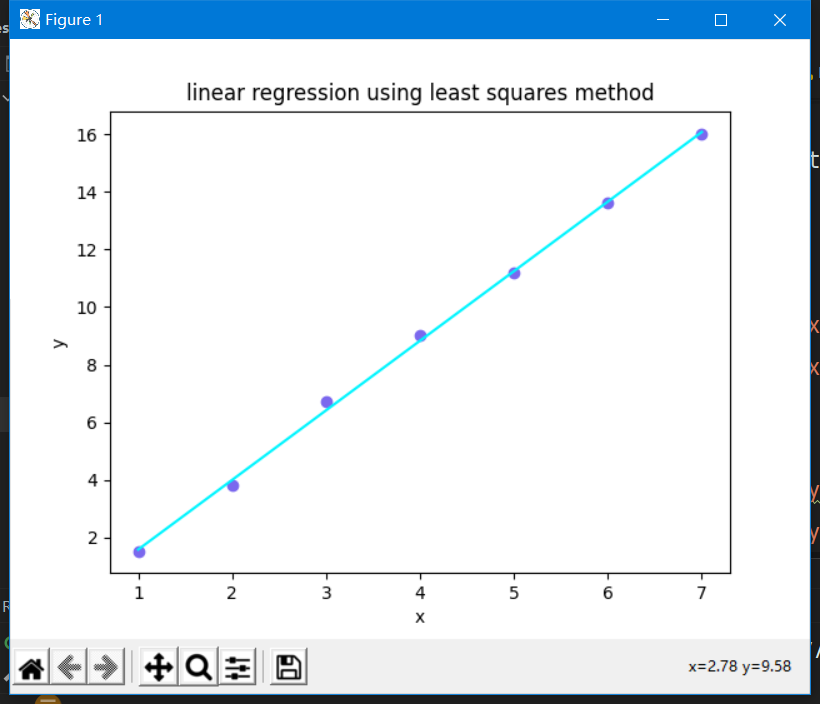
这篇文章主要是讲如何用最小二乘回归拟合直线。

我们的目标是计算直线方程中的值 m（斜率）和 b（y 截距）：

$$y=mx+b$$

Step

1.对于每个 $(x,y)$ 点计算 $x^2$ 和 $xy$

2.对所有 $x、y、x^2$ 和 $xy$ 求和，得到 $Σx、Σy、Σx^2$ 和 $Σxy$

3.计算斜率 m：

$$m = \frac{NΣ(xy) − Σx Σy}{N Σ(x^2) − (Σx)^2}$$

（N是点的个数）

4.计算截距 b：

$$b=\frac{Σy − m Σx}{N}$$

5.组装直线方程

$$y=mx+b$$

完成！

Python Code

import numpy as np
import matplotlib.pyplot as plt


def getSlope(n, x, y):
    return (n * np.sum(x * y) - (np.sum(x) * np.sum(y))) / \
           (n * np.sum(x ** 2) - (np.sum(x)) ** 2)


def getIntercept(n, x, y):
    m = getSlope(n, x, y)
    return (np.sum(y) - m * np.sum(x)) / n


x = np.array([1, 2, 3, 4, 5, 6, 7])
y = np.array([1.5, 3.8, 6.7, 9.0, 11.2, 13.6, 16])
n = len(x)

# 指定斜率和截距直线方程
y1 = getSlope(n, x, y) * x + getIntercept(n, x, y)

# 画图
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.scatter(x, y, c='#7B68EE')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_title('linear regression using least squares method')
ax.plot(x, y1, c='#00F5FF')
plt.show()

Result